Wanneer je de opdrachten met de parabool-applet hebt uitgevoerd, zal je dat een paar interessante conclusies hebben opgeleverd.
Bijvoorbeeld:
- Wanneer c kleiner is dan -2 of groter dan 0.25 , is er geen aantrekker, elke startwaarde gaat bij itereren naar oneindig.
- Wanneer c ligt tussen -0.75 en 0.25 is er een enkelvoudige aantrekker.
- Er is een dubbele aantrekker voor waarden van c tussen -0.75 en -1.25.
- Verlagen we de waarde van c nog verder, dan volgt er een klein gebiedje met een vierdubbele aantrekker, daarna een nog kleiner gebiedje met een achtdubbele aantrekker
(probeer c = -1.39 maar eens, als je die niet gevonden hebt)
- Maak je de c nog iets negatiever, dan stopt deze zogenaamde periodeverdubbeling en gebeurt er iets heel merkwaardigs: er is wel een gebied van startwaarden dat wordt aangetrokken, maar het itereren gaat niet naar een aanwijsbare (meervoudige) aantrekker toe. Er is geen enkele regelmaat meer te herkennen.
We noemen dit chaotisch gedrag en de aantrekker die er niet en toch ook wel is, noemen we een Vreemde Aantrekker. Rond dit chaotisch gedrag heeft zich een geheel nieuwe wetenschap ontwikkeld, de Chaostheorie.
- Nog merkwaardiger: in het chaosgebied zijn toch nog gebiedjes te vinden, waar wel een normale aantrekker is. Bijvoorbeeld in de buurt van c = -1.76 is er een driedubbele aantrekker!
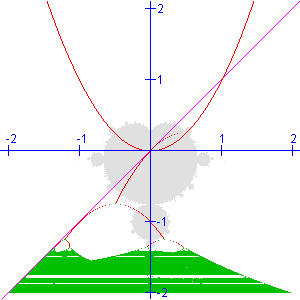 |
Al deze resultaten zijn samengevat in de grafiek hiernaast.
Toelichting:
Voor elke waarde van c zijn de aantrekkers als rode groene punten aangegeven op een horizontale lijn door c.
Bij voorbeeld: voor c = -1.00 hadden we een dubbele aantrekker gevonden: 0 en -1. Trek je een horizontale lijn door het punt y = -1 dan zie je dat die inderdaad de boom snijdt in de punten 0 en -1.
Trek je de horizontale lijn wat lager, dan passeer je een vertakking en krijg je vier snijpunten, etc.
Wat dieper begint de chaos: de hele lijn is groen.
Maar er zijn (meerdere) plaatsen, waar weer orde optreedt.
Die bij c = -1.76 is de grootste.
Voor c groter dan 0.25 of kleiner dan -2 treedt er in het geheel geen aantrekking meer op.
|
De groene figuur wordt de vertakkingsboom van Feigenbaum genoemd en is vernoemd naar de Amerikaanse wiskundige Mitchell Feigenbaum, die rond 1975 onderzoek deed op dit gebied. Wanneer je de monitor op zijn kop zet, lijkt het ook wel een beetje op een boom.
Deze Feigenbaum-boom is zelf een fractal! Je kunt dat zelf onderzoeken in de onderstaande applet.
Door in te zoomen (klik met de muis in de figuur) zul je ontdekken dat er in de chaos vele kleine gebiedjes van c-waarden zijn waar weer regelmatige aantrekkers zijn. En in die gebiedjes treedt opnieuw periodeverdubbeling op!
Op de schaalverdeling van de applet kun je de c-waarde aflezen. Wanneer je een c-waarde uit zo'n niet-chaotisch gebied, invoert in de parabool-applet van de vorige paragraaf, kun je controleren of de aantrekker daar ook echt gevonden wordt.
|